Hi,
Repeating Decimals are very interesting. We can express them as fractions, and also decimals with a line above the repeated numbers. Prior to this we could not define them mathematically as a fraction. With the formula a1/1-r we can. This is a very easy formula to use, and for things like 0.33333.... we just take (3/10)/1-(1/10) So then we can get 1/3. Overall, this is a very easy and helpful lesson. Hopefully it will show up more on the final because that would be enjoyable.
Thanks,
Kaili Chiu
So Many Choices!
Wednesday, April 29, 2015
Friday, April 24, 2015
Parametric Equations
Hello,
This week we learned about parametric equations. This is the first part of our calculus integration, and is a very simple topic. Parametric functions set parameters, and tell us the direction, start and end points. In solving, we are given two values, x and y. These are generally either given in trigonometric functions such as: sin(x), cos(x), tan(x), etc... There are other variations and transformations of these basic functions. When solving parametric equations, we do so by eliminating the parameter. By solving for t, we can substitute into the y= equation and eliminate the parameter. To graph them, we make a chart and plug in values in the range for "t". We can graph the xy points created by the table, and successfully graph the Parametric function.
Thanks,
Kaili Chiu
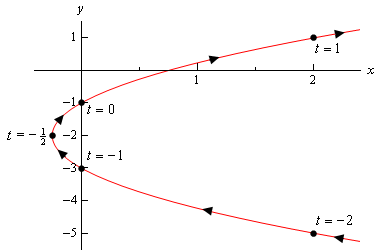
This week we learned about parametric equations. This is the first part of our calculus integration, and is a very simple topic. Parametric functions set parameters, and tell us the direction, start and end points. In solving, we are given two values, x and y. These are generally either given in trigonometric functions such as: sin(x), cos(x), tan(x), etc... There are other variations and transformations of these basic functions. When solving parametric equations, we do so by eliminating the parameter. By solving for t, we can substitute into the y= equation and eliminate the parameter. To graph them, we make a chart and plug in values in the range for "t". We can graph the xy points created by the table, and successfully graph the Parametric function.
Thanks,
Kaili Chiu

Friday, April 17, 2015
Partial fractions
Hi,
Today I will be talking about Partial Fractions. Partial fractions are the individual parts that create a fraction. In an example problem, we are asked to first identify whether the degree of the top is greater than the denominator. If it is greater, then we must use long division and take the partial fraction of the remainder. IF it is lesser than the denominator, we can skip this step and go to step 2. Step 2 is factoring the denominator. Once factored (if possible), we can add constants to the numerators of the factored parts. By solving for the constants, we can solve the Partial Fractions. Opposite to the saying "easier said than done", Partial Fractions are much easier to work out than I am explaining.
Kaili Chiu

Today I will be talking about Partial Fractions. Partial fractions are the individual parts that create a fraction. In an example problem, we are asked to first identify whether the degree of the top is greater than the denominator. If it is greater, then we must use long division and take the partial fraction of the remainder. IF it is lesser than the denominator, we can skip this step and go to step 2. Step 2 is factoring the denominator. Once factored (if possible), we can add constants to the numerators of the factored parts. By solving for the constants, we can solve the Partial Fractions. Opposite to the saying "easier said than done", Partial Fractions are much easier to work out than I am explaining.
Kaili Chiu

Subscribe to:
Comments (Atom)