Semester 2 Review

Hi Ms. V,

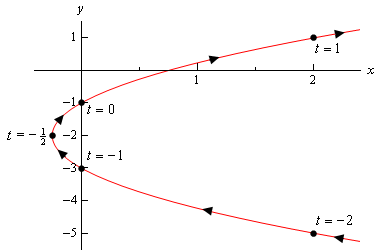
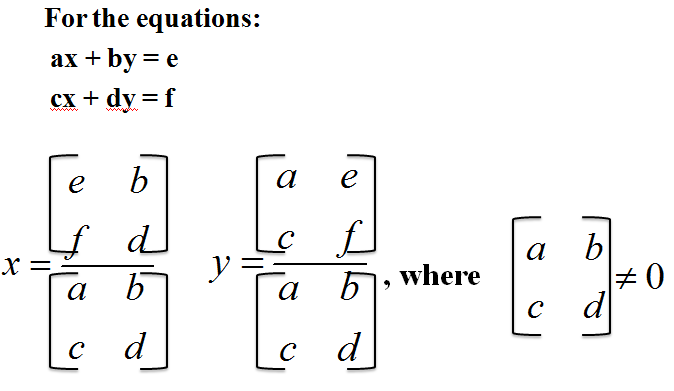Overall, in Semester 2, things were pretty interesting. We started off with less lessons than the first semester. We had Raymond read us Storytime for the first time, and it was hilarious. However, on the math end, towards the end of the semester, we started to do previews into calculus. Things like parametric equations and limits. Overall, second semester was pretty fun and interesting. Since this is the last blog we will do probably, I will take this time to say thank you for the wonderful years I've had in your class. I thoroughly enjoyed learning from you, even if webassign was a thing (just kidding). We ended with trigonometry, which we had previously somewhat covered. However, now we should be mastered in it.

Thanks for a great two years,

Kaili Chiu

Trig Review Week

Hello,

Today I will talk about trigonometry. Trigonometry can be a simple or hard topic to learn, depending on if one is comfortable with the identities and many other oddities in the subject. Some terms to for sure be familiar with are sine, cosine, tangent, cosecant, secant, and cotangent. These terms describe parts of a triangle. Sine is equivalent to the opposite side divided by the hypotenuse and so on and so forth. Trigonometry as we learned during this week uses certain identities to solve and verify trigonometric statements. In verifying, we are given an equation in which the left and right side are equivalent, although they have different variations, and we must manipulate only one side to make them both appear the same. In solving, we solve with the aid of identities and find answers in terms of angles of pi. Sometimes we are asked for a range or a general equation. The general equation just means that we must add a 2npi or npi depending on whether it is sine, cosines, or tangent.

That's all for today,
Kaili Chiu

Repeating Decimals

Hi,

Repeating Decimals are very interesting. We can express them as fractions, and also decimals with a line above the repeated numbers. Prior to this we could not define them mathematically as a fraction. With the formula a1/1-r we can. This is a very easy formula to use, and for things like 0.33333.... we just take (3/10)/1-(1/10) So then we can get 1/3. Overall, this is a very easy and helpful lesson. Hopefully it will show up more on the final because that would be enjoyable.

Thanks,
Kaili Chiu

Parametric Equations

Hello,

This week we learned about parametric equations. This is the first part of our calculus integration, and is a very simple topic. Parametric functions set parameters, and tell us the direction, start and end points. In solving, we are given two values, x and y. These are generally either given in trigonometric functions such as: sin(x), cos(x), tan(x), etc... There are other variations and transformations of these basic functions. When solving parametric equations, we do so by eliminating the parameter. By solving for t, we can substitute into the y= equation and eliminate the parameter. To graph them, we make a chart and plug in values in the range for "t". We can graph the xy points created by the table, and successfully graph the Parametric function.

Thanks,
Kaili Chiu

Partial fractions

Hi,

Today I will be talking about Partial Fractions. Partial fractions are the individual parts that create a fraction. In an example problem, we are asked to first identify whether the degree of the top is greater than the denominator. If it is greater, then we must use long division and take the partial fraction of the remainder. IF it is lesser than the denominator, we can skip this step and go to step 2. Step 2 is factoring the denominator. Once factored (if possible), we can add constants to the numerators of the factored parts. By solving for the constants, we can solve the Partial Fractions. Opposite to the saying "easier said than done", Partial Fractions are much easier to work out than I am explaining.

Kaili Chiu
 

Tower of Hanoi Puzzle

The tower of Hanoi was a very interesting way to learn about mathematical induction. By solving the ancient puzzle, we were able to understand recursive formulas and practice our finding the general formulas. According to the legend, a bunch of Brahmin priests found a temple with three posts surrounded by 64 gold disks. The prophecy explained that when the puzzle would be completed, the world would end. There are a certain set of rules, only one disk can be moved at a time, they have to be in decreasing order from top to bottom, and you can only take the top disk from the pile when moving. Whilst trying to solve the puzzle, I noticed a certain pattern. In order to get the rings to the last pole, I had to put the first ring on the middle rung and then larger one on the last. This would allow me to place them in increasing size order. The number of moves can be determined by the formula (2^n)-1. This formula will work for any number of disks, and with this formula we can calculate that the priests would have to be doing the puzzle for 585 billion years. At least now we know that the world is safe!

Graphing Systems of Inequalities

Hi,

Systems of Inequalities is very interesting, because it is a review topic. Generally we've finished a lot of the systems of inequalities, but now we are touching over it again. When graphing systems of inequalities, graph it without the inequality and fill in the inequality. It's generally pretty easy to do. However we must remember to observe the rule: when dividing by a negative, we must flip the inequality sign. Sometimes it is easy to make careless errors, but most of the errors will be made in the algebra. The solution will be located in the shaded part.

Thanks,
Kaili Chiu

Cramer's Rule

Hello,

Today I will talk about Cramer's rule. Cramer's rule involves using matrices to solve systems of equations. A quick refresher on matrices: finding the determinant of a 2x2 is ad-bc. Finding the determinant of a 3x3 involves making smaller 2x2's and finding the minors or determinants of those. Substitute the solution column for each variable, finding the determinant of the new matrices formed. Dx/D = x value, Dy/D = y value, and Dz/D = z value. This will solve your equation and allow you to find your answer. Not so hard was it?

Thanks,
Kaili Chiu

Sequences and Series

Hi,

Generally sequences and series was pretty annoying. Especially the card problems, they were tough. Overall, there were many formulas to this, and we also had things like permutations and combinations. These were pretty easy, but when combined in word problems, they were really hard. Honestly, I had a little trouble with them. Overall though, after this week I feel confident in sequences and series. The test was a bit tough though. I will definitely need to review them in the future.

Thanks,
Kaili Chiu

Systems of equations.

Hello,

Today I will be covering systems of equations. Systems of equations are a collection of multiple equations with solutions. These systems can be consistent or inconsistent, and if they are consistent it means that they have a solution, and if they are inconsistent, it means that they have no solution. If they are consistent, they have the option be be either dependent or independent. If they are dependent, it means that the solutions are zero, and you must solve for z and substitute z for t. Independent solutions mean that they are real numbers greater or less than 0. We can solve systems of equations using elimination or substitution or even matrices.

Thanks,
Kaili Chiu

Graphs of Polar Equations

Hi,

Graphing Polar Equations is quite a task. We have to first master polar coordinates, which was explained in the previous blog post. Now that we've reviewed that, we can take a look at the graphs. We use the conversions of r^2 = x^2 + y^2. and x=rcos(theta) and y=rsin(theta). A circle could be r=asin(theta). There are limacons, cardioids, rose curves, and lemniscates. We played around with them in class, when we made art to create a picture. Overall it was a pretty cool lesson, and I enjoyed it a lot.

Thanks,
Kaili Chiu

Polar Coordinates

Hello,

Today, I will talk about Polar Coordinates. Polar coordinates are on a different plane than the (x,y) coordinates. (x,y) coordinates are on the Cartesian plane, whereas the Polar coordinates are on a polar plane. Instead of the common (x,y) point, on the polar plane it is (r,θ). θ is the angle at which the axis is rotated in relation to the positive x-axis of the cartesian plane. Although this seems very confusing at first, it is only just tedious. All in all, though intimidating, this lesson was quite easy.

Thanks,
Kaili Chiu

Rotating Conic Sections

Hello,

Conic sections can be rotated around the origin, substituting x prime and y prime for x and y. We can use unit circle measurements to find the angle. Using the unit circle measurements for the angle, we can adjust the entire cartesian plane to rotate the graph. Some useful information on rotating conic sections include knowing basic trigonometry such as x=xprimecos(theta)-yprimesin(theta), and the y point. These allow the student to plug x and y points into the original formula given. The result will be the rotated equation. Simplify and turn in your answer!

Thanks,
Kaili Chiu

Parabolas

Hello,

Today I am going to talk about parabolas. They are quadratic graphs and are shaped like a "u", although if the standard form is negative, it is shaped like an "n". The a value in standard form determines the opening up or down, and if a>0, then it opens up, and if a<0, it opens down. Parabolas have a vertex, a focus, and a directrix. On a regular (x-h)^2 = 4c(y-k) graph, (h,k) is the vertex, (h, k+c) is the focus, and h-c is the directrix. The axis of symmetry is on the same x coordinate as the vertex of a standard parent graph. Parabolas are present in many fields, including physics and engineering.

Thanks,
Kaili Chiu

Semester 2 Goals

Hi,

There are some things I did well in last semester. These were memorizing the trig identities, and trying to keep my grade up in the end of the semester. In addition, towards the end of the semester, I started to really focus on how the pieces in the sections of the chapter fit together to apply concepts. however, there are inevitably some things I did poorly in. Some of these included forgetting to finish homework, forgetting to take notes in class, and procrastinating. I would really like to fix these problems, and the only way I can do that is to put in hard work. During Christmas break, there wasn't anything really funny, but the only thing that could be funny is that my cousin came over and accidentally went to the neighbors house.