Tangent

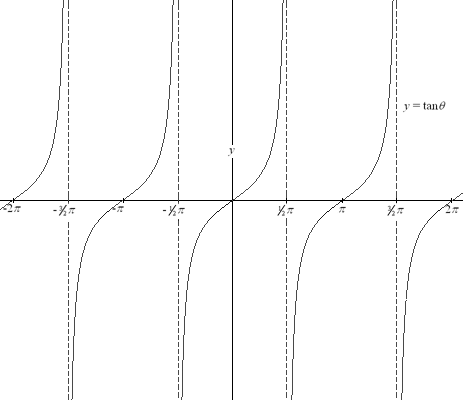
Tangent is a very interesting operation. It is the brother of cosine and sine, and involves both of them in its composition. Sine over cosine equals tangent, or opposite over adjacent. As can be assumed from the previous blog post, tangent is found in right triangles. Even more interesting, the tangent graph has asymptotes. Its counterpart is cotangent, or 1/tan on a calculator or in a calculation. However, tangent is also a term used to mean touching at one point.

Sine and Cosine

Sine and cosine are two of the 6 important operations that one can perform on triangles. However, the only type of triangles one can use these two on is right triangles. Right triangles have one angle of 90 degrees, and using sine and cosine, we can find missing sides or angles. Sine and cosine on a calculator are represented by sin and cos. Sine is equal to the opposite side over the hypotenuse, whereas the cosine is equal to the adjacent side over the hypotenuse. Additionally, on a unit circle and also cartesian plane, cosine is equal to the x value, whereas the sine value is equal to the y value. We can use these to substituted x and y values and find specific lengths.

Chapter 3 Summary

Chapter 3 was all about functions. This involved rational functions, complex numbers, and factoring. We used many methods to solve and factor, like the foiling method, quadratic formula. Also, we found zeroes, which are the solutions of a function. An example of a quadratic function is f(x) = 4x^2 + 2x - 6.
The zeroes of this function can be found using the quadratic formula, or [-b +/- sqr(b^2 - 4ac)]/2a. When you plug in the values for the function, you get two solutions because of the +/- sign. This is where 4 = a, 2 = b, and -6 = c. Overall this was a very interesting chapter, although it is review.

Rational Functions

Hello,

Rational functions, the amazing nature of them. First, we learned about Rational functions in a test. This is called the Rational Zero Test, and is represented in p/s = factors of constant/factors of leading coefficient. The constant is the number at the end of function, and the leading coefficient is the coefficient of the biggest degree of the variable. When one of these works in f(x), you can use synthetic division to find the equation and eventually factors. Next, we used the midpoint equation to estimate a point to the utmost accuracy. Lastly, we understood rational functions and finding certain points and parts to a function. We found holes, asymptotes, x and y intercepts.

Thanks,
Kaili Chiu