So Many Choices!
Friday, November 21, 2014
Mr. Unit Circle
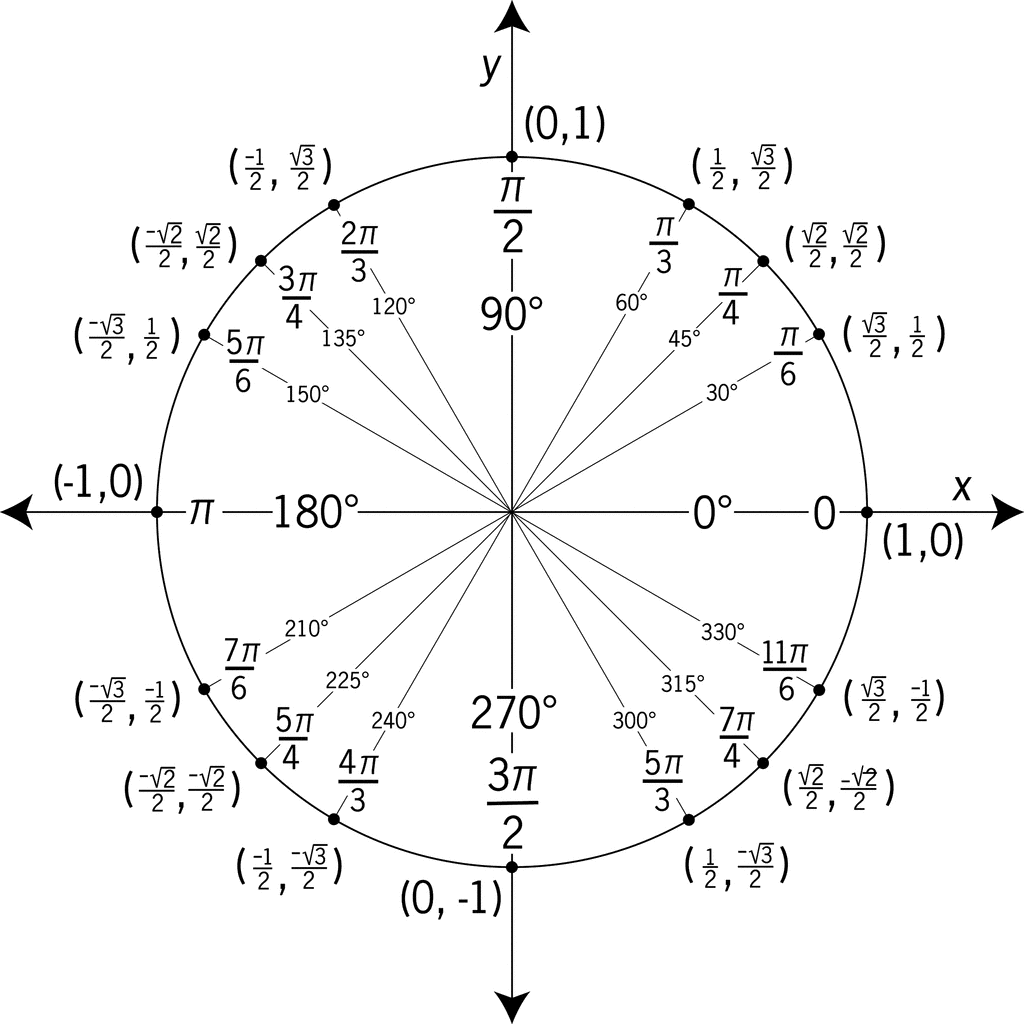
The unit circle is a very useful tool. It has a radius of 1, and shows the x and y values along the circumference. Using special case angles, we can find the lengths and values of right triangles that have one of the special angles. Again, cosine and sine come into play, as cosine=x value, and sine=y value. We can use the acronym ASTC, all students take calculus, which helps remember which function is positive in which quadrant. A is all, S is sine, T is tangent, and C is cosine. We made our own unit circles in class using paper plates, and we drew all the angles and also radian measures on them. This was very useful on the test, and saved lots of time!


Wednesday, November 19, 2014
Chapter 4 Overview
Hi,
Today I will be talking about chapter 4. This chapter was very long, consisting of 10 lessons of trigonometry. However, it was very interesting, relating the sides of triangles to the unit circle, which accounts for special triangles and angles. The things to remember are (cos,sin) = (x,y), and cosine is equivalent to adjacent side over hypotenuse, whereas sine is opposite over hypotenuse and tangent is opposite over adjacent. This information allows us to find the points along the unit circle, finding the coordinates along the circumference using 45-45-90 and 30-60-90 right triangles sine and cosine values. Additionally, we learned that trigonometry has many identities, which are tools used to interpret and manipulate trigonometric equations for solving. We can prove the existence of these identities using verifying. Lastly, inverses are for solving for arcsin1/2 and we are solving for x. We solve by taking the sin^-1 of 1/2 and that is x.
Thanks,
Kaili Chiu

Today I will be talking about chapter 4. This chapter was very long, consisting of 10 lessons of trigonometry. However, it was very interesting, relating the sides of triangles to the unit circle, which accounts for special triangles and angles. The things to remember are (cos,sin) = (x,y), and cosine is equivalent to adjacent side over hypotenuse, whereas sine is opposite over hypotenuse and tangent is opposite over adjacent. This information allows us to find the points along the unit circle, finding the coordinates along the circumference using 45-45-90 and 30-60-90 right triangles sine and cosine values. Additionally, we learned that trigonometry has many identities, which are tools used to interpret and manipulate trigonometric equations for solving. We can prove the existence of these identities using verifying. Lastly, inverses are for solving for arcsin1/2 and we are solving for x. We solve by taking the sin^-1 of 1/2 and that is x.
Thanks,
Kaili Chiu

Wednesday, November 12, 2014
Trigonometric Functions
Hi,
Today I am going to talk about Trigonometric functions. These are dealing with lots and lots of triangle values. cosine, sine, and tangent, as well as their reciprocal functions are found using identities and a useful acronym SOHCAHTOA. When solving trig functions, one can perform many algebraic tricks and action such as factoring and the quadratic formula. If one was to solve say sinx=1/2, we could find a series of angles in 0 to 2pi. Overall, this is a very interesting way to look at triangles. The pythagorean theorem even factors into how the identities are derived!
Thanks,
Kaili Chiu

Today I am going to talk about Trigonometric functions. These are dealing with lots and lots of triangle values. cosine, sine, and tangent, as well as their reciprocal functions are found using identities and a useful acronym SOHCAHTOA. When solving trig functions, one can perform many algebraic tricks and action such as factoring and the quadratic formula. If one was to solve say sinx=1/2, we could find a series of angles in 0 to 2pi. Overall, this is a very interesting way to look at triangles. The pythagorean theorem even factors into how the identities are derived!
Thanks,
Kaili Chiu
Friday, November 7, 2014
Verifying Identities
Hi,
Today, I am going to be talking about verifying identities. This is a very complex topic, as it is basically proving the identities in various situations of trigonometric functions. There are a bunch of tips and rules. First, you can only work on one side of the graph. Two, it is suggested that you pick the more complicated side, although when checking your work, you could use the other side. Another tip is to remember the algebra tricks such as grouping and multiplying by the conjugate. When you've mastered all of these tips and tricks, you will be able to verify!
Thanks,
Kaili Chiu
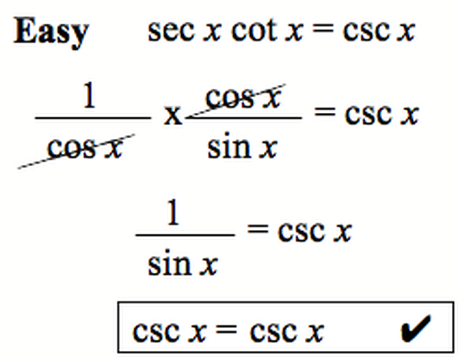
Today, I am going to be talking about verifying identities. This is a very complex topic, as it is basically proving the identities in various situations of trigonometric functions. There are a bunch of tips and rules. First, you can only work on one side of the graph. Two, it is suggested that you pick the more complicated side, although when checking your work, you could use the other side. Another tip is to remember the algebra tricks such as grouping and multiplying by the conjugate. When you've mastered all of these tips and tricks, you will be able to verify!
Thanks,
Kaili Chiu

Subscribe to:
Comments (Atom)