Hi,
My name is Kaili Chiu. I am 15 years old, and my birthday is January 20, 1999. Throughout my early life (from 5-11) I was a happy child, and was very interested in the sport of Archery. I picked up the sport and progressed, shooting in competitions such as the Nationals. Throughout my 15 years, my parents, Lihu and Lucille have been caring, understanding, and patient, teaching me essential lessons and instilling morals. My sister of 13 years is very mature, and is often mistaken to be older than me, competitive, and artistically and musically gifted. When I was 4, I enrolled in High Point Academy, a Primary School from grades 1-8. At around the grade 6, I picked up the sport of Golf, and was intrigued by the complex nature of the activity. To this day, I still play golf for the Maranatha Golf Team, and am happy with my life at the moment. I enjoy other interests like art, music, and video games, although for most days out of the year, I attend a Christian school called Maranatha High School.
Thanks,
Kaili Chiu


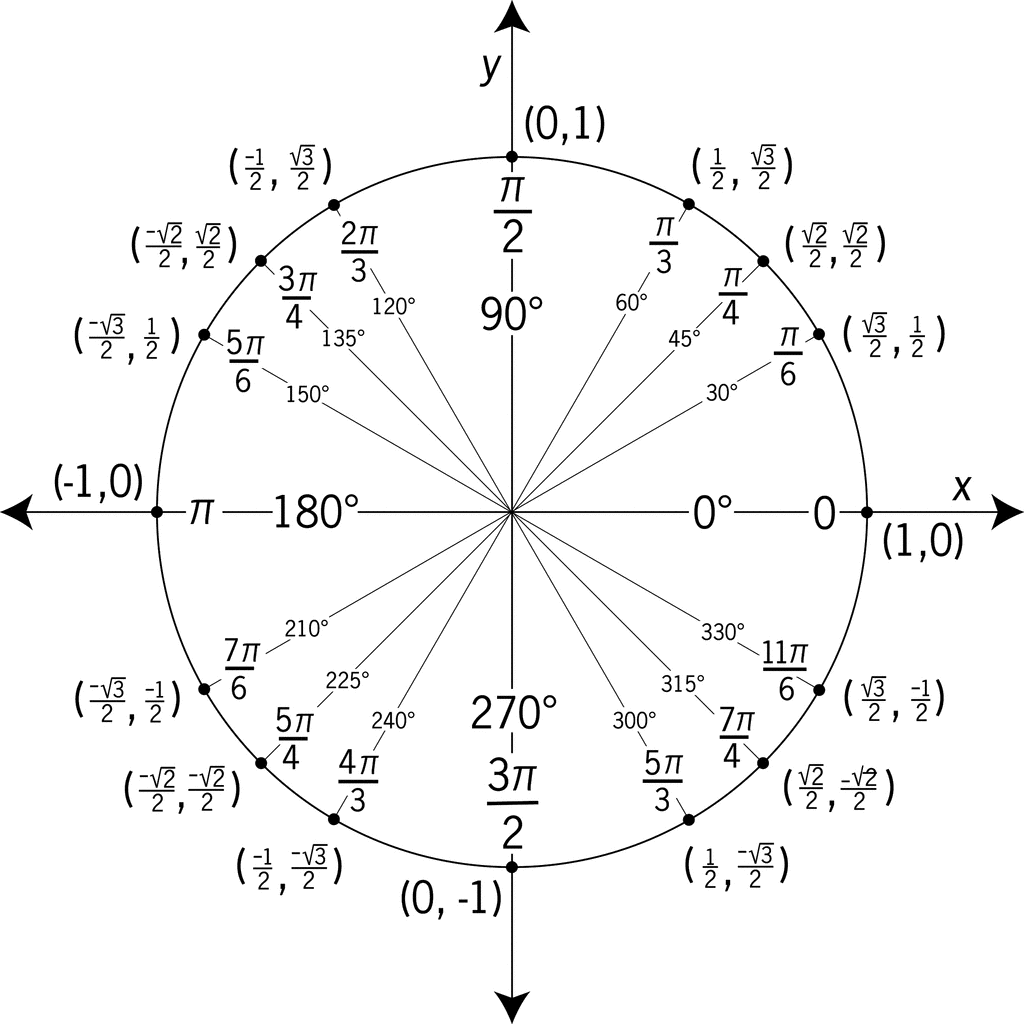

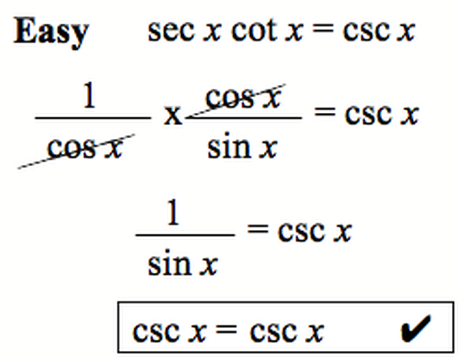
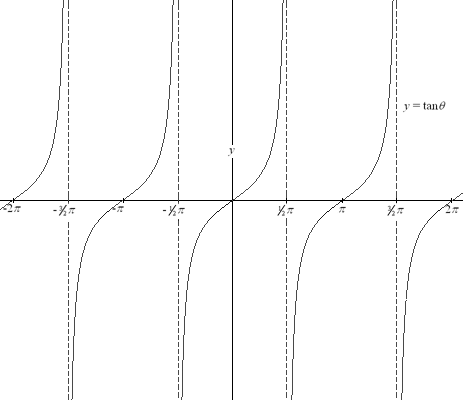













.JPG)